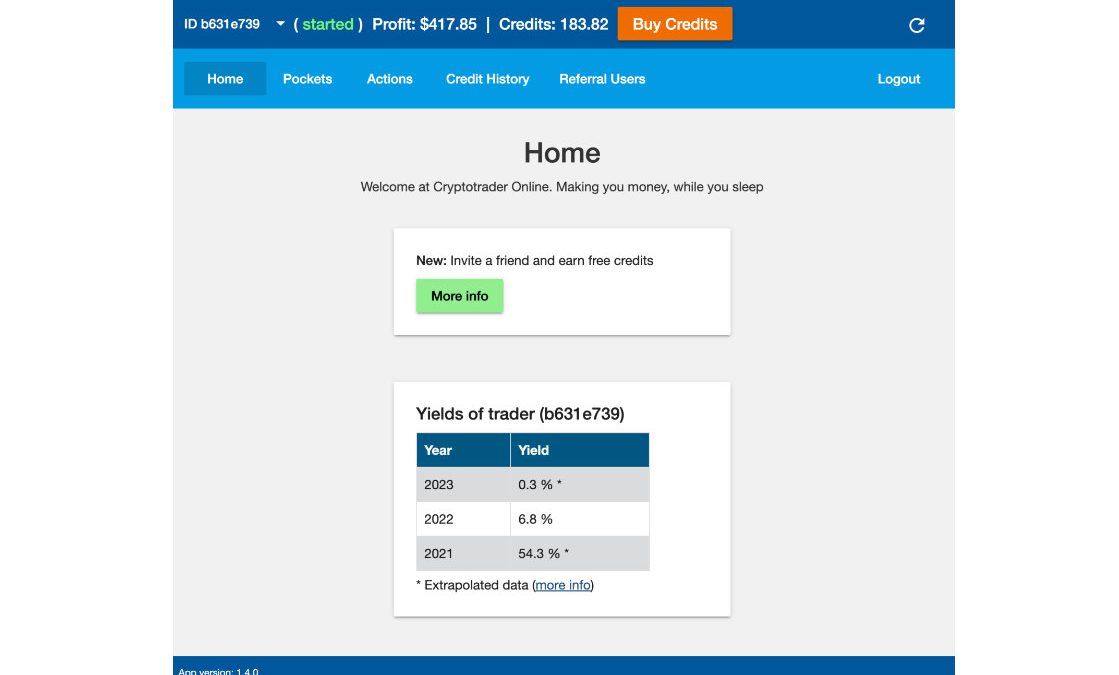
In the new Cryptotrader web app, every user can see the yields of his own trader. Returns depend among other things on price movement, entry time and capital; past performance is no guarantee. See also the FAQ.
Returns
The yield is calculated based on the profit in relation to the invested capital. We make this calculation separately for each trader. Average calendar-year returns of existing users are on Returns.
